|
|
угловая частота
Скорость изменения фазы синусоидального электрического тока, равная частоте синусоидального электрического тока, умноженной на 2π.
Примечание — Аналогично определяют угловые частоты синусоидальных электрического напряжения, электродвижущей силы, магнитного потока и т. д.
[ГОСТ Р 52002-2003] |
|
EN |
angular frequency
pulsatance
ω
product of the frequency of a sinusoidal quantity and the factor 2π
NOTE – For the quantity Am cos (ω t + θ0), the angular frequency is ω.
[IEV number 101-14-36 ] |
|
FR |
pulsation
produit de la fréquence d'une grandeur sinusoïdale par le facteur 2π
NOTE – Pour la grandeur Am cos (ω t + θ0), la pulsation est ω.
[IEV number 101-14-36 ] |
Практика остановила свой выбор на синусоидальных колебаниях переменных электрических величин. В дальнейшем, говоря о токе, э. д. с., напряжении и магнитном потоке, мы будем считать их изменяющимися по закону синуса.
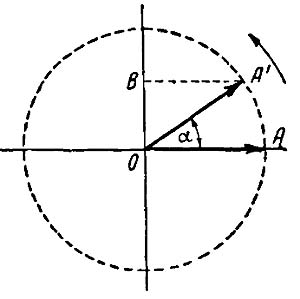
Фиг. 130. Вращение вектора вокруг оси
Пусть мы имеем вектор ОА (фиr. 130), выражающий в масштабе какую-либо переменную синусоидальную величину, например ток. Будем вращать с постоянной скоростью вектор вокруг точки О против часовой стрелки. Конец вектора будет описывать окружность, а угол, на который поворачивается вектор, будет меняться с течением времени.
Угловая скорость или угловая частота ω (омега) вращения равна углу поворота вектора в единицу времени: ω=α/t, откуда α=ωt.
Часто вместо градуса пользуются другой единицей измерения угла – радианом. Радианом называется угол, дуга которого равна радиусу. Если длина окружности С=2πR, то она содержит 2πR/R=2π радиан.
За один оборот радиус-вектор ОА будет иметь один период вращения продолжительностью Т секунд.
Угловая частота в этом случае выразится: ω=α/t=2π/T рад/сек.
Так как 1/Т=f, то ω=2πf рад/сек.
[Кузнецов М. И. Основы электротехники. М, "Высшая Школа", 1964]
